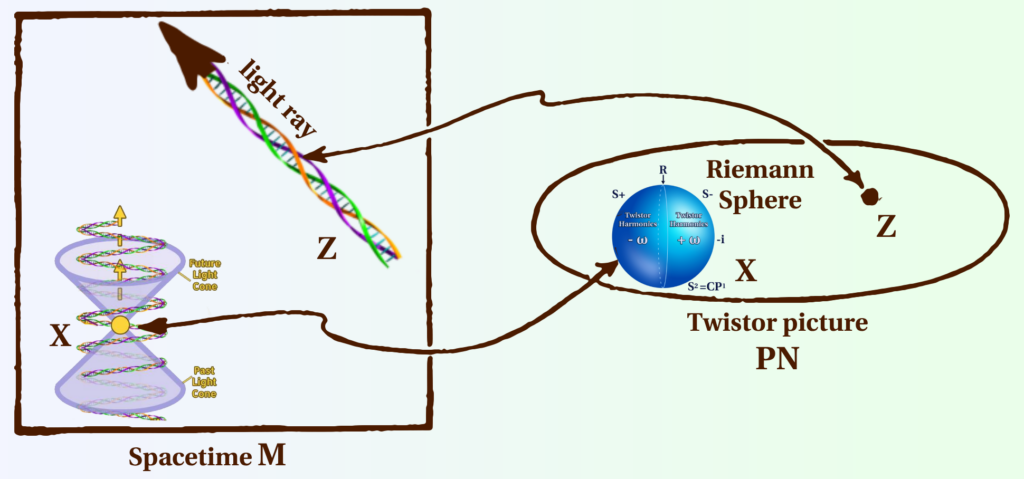
Twistor theory represents a profound reformulation of the geometric structure underlying space-time, merging complex analysis with fundamental physical principles. Originally developed by Roger Penrose in the 1960s, the theory has evolved into a powerful tool for understanding scattering processes, integrable systems, and potential pathways to a quantum theory of gravity (Penrose, 1967)​.

The Mathematical Foundations of Twistor Space

Twistor theory is built on the notion that space-time points can be recast as elements of a complex projective space. In conventional Minkowski space, events are described by real coordinates, whereas in twistor space each point corresponds to a light ray or null geodesic. This reinterpretation offers several advantages:

• Complex Geometry: The use of complex variables allows the transformation of differential equations governing classical fields into problems in complex geometry and algebraic geometry (Atiyah & Ward, 1977)​.
• Projective Structures: By embedding space-time into a higher-dimensional complex projective space, twistor theory provides a natural setting to explore conformal invariance and other symmetries that are less apparent in standard formulations.

The Penrose Transform and Field Equations

Central to the application of twistor theory is the Penrose transform, which establishes a correspondence between solutions of massless field equations in space-time and cohomology classes in twistor space. This mapping has significant implications:

• Unification of Equations: The transform converts differential equations—such as the zero-rest-mass field equations—into problems in sheaf cohomology, offering new methods to solve them (Penrose & Rindler, 1984)​.
• Simplification of Scattering Amplitudes: The reformulation in twistor space has led to considerable progress in calculating scattering amplitudes in gauge theories, where conventional perturbative methods become unwieldy (Witten, 2004)​.

Applications in Modern Theoretical Physics

The implications of twistor theory extend into several areas of high-energy physics and mathematical physics:

• Scattering Amplitudes: In the realm of quantum field theory, twistor-inspired methods have revolutionized the calculation of scattering amplitudes. By reformulating interactions in terms of twistor variables, researchers have derived compact expressions for amplitudes that were previously intractable (Mason & Skinner, 2009)​.
• Integrable Systems: The inherent symmetries of twistor space have provided new insights into the study of integrable systems. These connections offer promising avenues for understanding non-perturbative phenomena in field theory.
• Quantum Gravity: Although a complete theory of quantum gravity remains elusive, twistor theory offers a framework that could bridge the gap between general relativity and quantum mechanics. Its emphasis on conformal structures and complex geometry is seen as a potential stepping stone towards a unified theory (Penrose, 2004)​.

Scientific References and Further Reading

For those interested in a deeper exploration of twistor theory, the following references provide comprehensive discussions and mathematical details:

1. Penrose, R. (1967). Twistor Algebra. This seminal paper laid the groundwork for the development of twistor theory.
2. Atiyah, M., & Ward, R. (1977). Twistor Geometry and the Einstein Equations. An important work that connects twistor theory with solutions to Einstein’s field equations.
3. Penrose, R., & Rindler, W. (1984). Spinors and Space-Time, Volume 1: Two-Spinor Calculus and Relativistic Fields. A detailed exposition of the mathematical tools used in twistor theory.
4. Witten, E. (2004). Perturbative Gauge Theory as a String Theory in Twistor Space. A groundbreaking paper linking twistor methods with modern approaches to scattering amplitudes.
5. Mason, L., & Skinner, D. (2009). Twistor Strings and the Scattering Amplitudes. This work extends the application of twistor theory to modern scattering amplitude computations.

Concluding Remarks

Twistor theory remains an active and vibrant area of research in mathematical physics. Its ability to reformulate complex field equations into more tractable geometric problems continues to inspire new methodologies and insights in both mathematics and physics. As investigations progress, the integration of twistor methods with contemporary approaches may yet unlock further secrets of the quantum structure of space-time.