Time Crystals 2025 – The Twistor

Subject: Time Crystals Conference

Dear Participant,

We regret to inform you that your application to attend the Time Crystals Conference has not been accepted.

We appreciate your interest in the conference and thank you for the time and effort you put into your submission.

Best regards,

Conference Chairs:
Rosario Fazio
Krzysztof Sacha
Giuseppe Strangi

String Time Crystals

Dr Tadeusz Habdank, CEO at PINS; Julianna Habdank, Student at IU Internationale Hochschule.

**Twistor Theory Concepts**

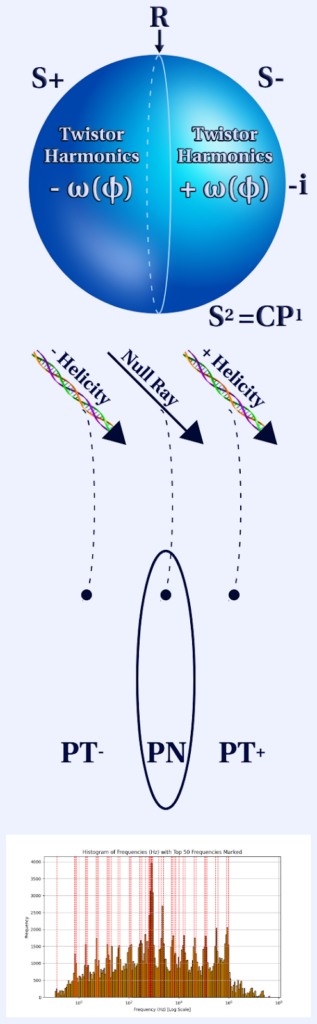
**Riemann Sphere (S² = CP¹):** Represents the complex projective line with both positive and negative frequency functions, where **S⁺ and S⁻** denote positive and negative frequency components of waves or fields.

**+helicity / -helicity:** Indicate particle helicity, showing spin alignment with or against momentum.

**PT⁺, PT⁻, and PN:** Represent twistor space regions: positive (PT⁺), negative (PT⁻), and the null (PN) or transitional region between them.

String Time Crystal [1] is a mental shortcut describing the concept of combining string theory in its application to support the creation of an applicational systematics of time crystals. Elements of this theory, especially in the twistor string approach, may allow for the creation of a basic framework for the formulation of a new approach to the model systematics of time crystals, inspired by the works of Frank Wilczekand Sir Roger Penrose [2]. The foundations for building a model describing the String Time Crystal (STC) concept include the use of topological algebra inspired by string theory, the support of the Penrose transform for dimension reduction, the definition of the framework for the construction of Fourier space and its parameters, and an attempt to simulate this concept using quantum computing methods.

Extending this twistor-string perspective [3], we introduce a Twistor Spectral Space, a mathematical structure in which discrete time-translation symmetry is initially encoded before its spontaneous breaking occurs. This approach leverages the geometric properties of twistor theory, where periodicity in time evolution is naturally embedded in twistor coordinates. By examining twistor holonomy conditions and the frequency function analysis of twistor wavefunctions, we provide a systematic classification of subharmonic responses that characterize time-crystalline behavior. Furthermore, twistor frequency decompositions serve as an essential bridge between twistor-string methods and the time-crystalline phase structure in many-body quantum systems.

Complementing this twistor-geometric formulation, we construct a Quantum Fourier Frequency Space, which enables the isolation of subharmonic responses through quantum Fourier analysis [4]. This frequency-space methodology correlates distinct frequency components with underlying quantum interactions, offering a deeper insight into the interplay between many-body interactions, disorder, and emergent non-equilibrium phases. These insights serve as a foundation for advanced simulation techniques, which could potentially be realized using quantum computations.

Additionally, we extend our analysis through Spinor Frequency Analysis and Spectral Characterization, where we investigate the governing equations of spinor frequency functions. This spectral approach allows us to quantitatively resolve repeatable spectral peaks observed in time crystals, uncovering the shape and inter-peak distances of these structures. This deeper understanding of quantum dynamics and emergent stability mechanisms further refines the theoretical systematics of time crystals.

Through the integration of twistor-string methods, Fourier-based spectral decomposition, and spinor frequency analysis, we propose a comprehensiveframework for exploring exotic phases in driven quantum systems. The STC theory not only provides a systematic classification of time-crystalline phenomena but also opens avenues for practical implementation in quantum computing and fundamental physics, potentially leading to novel applications in quantum control and information processing.

Within this formulation, spatial and frequency structures are described by the multi-dimensional coordinate representation x=(x¹,x²,…,xⁿ), capturing the geometric complexity of twistor space and frequency function scaling N(r)≈λr that establishes a direct link between eigenvalue spectra and the oscillatory structures characteristic of time-crystalline behavior [5].

x ~ n-dimensional point on the manifold M;
N(r) ~ Frequency function, r ~ Scale parameter, λ ~ Frequency parameter in twistor space;

[1] https://timecrystalesa.com/

[2] Dunajski, M., & Penrose, R. (2023). Quantum state reduction, and Newtonian twistor theory. Annals of Physics, 451, 169243. https://doi.org/10.1016/j.aop.2023.169243

[3] Atiyah, M., Dunajski, M., & Mason, L. J. (2017). Twistor theory at fifty: From contour integrals to twistor strings. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 473(2206), 20170530. https://doi.org/10.1098/rspa.2017.0530

[4] Szczeciniarz, J.-J., & Kouneiher, J. (2022, September 19). Regards and insights on the universe: Sir Roger Penrose’s mathematical-physics works and philosophy (1). Annals of Mathematics and Philosophy, 1 Szczeciniasz, Kouneiher (2022)[5] Borrelli, W., & Wu, R. (2023). On the nodal set of solutions to Dirac equations. arXiv. https://doi.org/10.48550/arXiv.2312.0791